1.   引言

高光谱图像（Hyperspectral Image， HSI）是由成像光谱仪获取，通过单次采集记录勘测场景数百甚至数千个光谱波段的遥感数据^［1］。由于其丰富的光谱信息，HSI已被应用于许多领域，包括目标识别、军事防御和地表矿物勘测等^［2］。由于地物对象的复杂性和相对较低的空间分辨率，HSI中的像元通常由多个地物光谱混合而成^［3］，导致混合像元现象产生，这种现象影响了高光谱分析的性能，阻碍了HSI的应用。为解决这个问题，高光谱分解技术被广泛用于识别混合像元中的纯地物成分并估计每个混合像元中各类纯地物所占的比例，这两个过程称为端元提取和丰度反演^［4］。

现有的混合模型分为线性模型（Linear mixture model， LMM）和非线性模型（Nonlinear mixture model， NLMM）两种^［5］，虽然NLMM可以解释特定场景中发生的多重散射效应，但在多数情况下通常认为LMM是测量过程中更为合理的混合模型^［6］，因此基于LMM的解混算法备受关注。一般来说，分解算法可以分为4类：几何方法、基于稀疏回归的方法、统计方法和基于深度学习的方法^［7］。

几何算法假设HSI的端元是包含数据集的凸单纯形的顶点，经典的算法有顶点成分分析^［8］、最小体积单形体分析^［9］和迭代限制端元法^［10］等。基于稀疏回归方法是将场景中的混合像元表示为现有光谱库中部分光谱的线性组合，通过估计对应丰度以实现解混。统计方法利用HSI的统计特性，同时提取端元并估计丰度。流行的统计算法包括独立成分分析^［11］和非负矩阵分解（Nonnegative Matrix Factorization，NMF）^［12］等。其中，NMF由于其非负性和良好的可解释性，非常契合高光谱解混。为寻求更好的解混性能，近年来众多基于NMF的方法被提出。

然而，基于NMF的解混模型是非凸的，导致算法在优化过程中容易陷入局部最小，限制了解混的性能。为了减小解空间，各种额外约束被加入到NMF模型中，常见方法是构造针对丰度和端元的约束项。MIAO等人^［13］通过研究端元集的固有结构，将最小体积约束加入到NMF中，有效地从高度混合的高光谱数据中提取端元。QIAN等人^［14］通过在NMF模型上加入L_1/2正则器作用于丰度，得到了比L₁正则器更稀疏的结果。由于该策略简单有效，L_1/2正则器被广泛应用于开发新的解混方法。根据端元相互独立的特性，陈善学等人^［15］将正交约束作用于端元并加入到NMF模型中，结合L_1/2正则器，保证了丰度稀疏性的同时增强了端元光谱的独立性，提高了端元提取的有效性。文献［16］在正交约束的基础上引入再权重稀疏丰度正则项，进一步提高了丰度的稀疏性。WANG等人^［17］通过引入双权重共同约束丰度，从端元和像元的角度增强了丰度的行稀疏性和列稀疏性。以上方法虽然获得了不错的解混性能，但都忽略了对高光谱图像的空间先验信息的利用。ZHANG等人^［18］引入空间图正则项来捕获高光谱数据的空间流形结构，并构造空间权重因子来挖掘像元间的空间相关性，充分利用了空间信息。QU等人^［19］结合一阶和二阶像元最近邻关系构造高阶拉普拉斯图正则项，更好地保留了图像的全局空间结构，增强了高光谱图像同质区域的聚合。文献［20］引入子空间结构正则项来捕获高光谱图像矩阵的固有内在结构，从而获取全局空间分布信息，得到了较好的解混结果。文献［21］中引入光谱权重因子提升了丰度的稀疏性，并结合空间邻域结构构造空间权重因子促进了丰度的平滑性。尽管这些方法取得了一些成果，但由于传统的NMF模型对噪声和异常值比较敏感，影响了解混效果。基于此，TANER等人^［6］提出了一种改进的NMF模型，通过引入残差权重因子，根据迭代的重构残差来调整损失函数每一行的贡献权重，有效减轻了噪声的影响，提升了算法的鲁棒性。此外，一些研究聚焦于将NMF与深度学习相结合，FENG等人^［22］将NMF模型扩展为深度NMF模型，并利用光谱和空间信息约束丰度，通过预训练和微调每层权重，得到了不错的解混性能。LI等人^［23］提出了一种鲁棒自监督深度解混模型，通过利用深度自编码器，有效降低了噪声的影响。

为改善基于NMF模型的解混算法鲁棒性较差、解混精度不佳的问题，本文提出了一种基于自适应空谱约束的加权残差非负矩阵分解高光谱解混算法（Weighted Residual NMF for Hyperspectral Unmixing Under Adaptive Spatial-Spectral Constraint， ASSC-WRNMF）。首先，将残差权重因子加入到损失函数中，改进传统NMF模型，其次，为利用高光谱图像丰富的空间信息，通过引入像元空谱相似度来捕获像元间的联系，以此确定像元邻域，并通过邻域构造空间权重因子，促进丰度的平滑性。同时结合光谱权重因子，增强丰度的稀疏性。此外，结合端元的物理特性，引入端元平滑约束，调整端元的平滑程度。最后，推导乘法更新规则，以此更新端元矩阵和丰度矩阵。

2.   非负矩阵分解

2.1   线性光谱混合模型

本文提出的ASSC-WRNMF算法基于LMM。LMM假设像元的光谱是由端元光谱的直接线性混合形成的。假设一幅高光谱图像表示为$\mathit{Y}=[{\mathit{y}}_{\mathrm{1}},\cdots ,{\mathit{y}}_N]\in {\mathbf{R}}^{L\times N}$，其中${\mathit{y}}_i$是$L$维列向量，代表第$i$个像元光谱，$L$是波段数，$N$表示图像中的像元数。由此，基于LMM的高光谱图像可以表示为：

其中，$\mathit{E}\in {\mathbf{R}}^{L\times n}$表示端元矩阵，包含$n$个端元（每一列代表一个端元光谱），${\mathit{a}}_i=[a_{i\mathrm{1}},\cdots ,a_{in}{]}^{\mathrm{{\rm T}}}$表示${\mathit{y}}_i$的丰度向量，${[\cdot ]}^{\mathrm{T}}$表示转置运算，$\mathit{p}$为噪声。如用矩阵表示，高光谱图像$\mathit{Y}$可以描述为：

其中，$\mathit{A}\in {\mathbf{R}}^{n\times N}$表示丰度矩阵，$\mathit{P}\in {\mathbf{R}}^{L\times N}$表示噪声矩阵。因为丰度的物理意义是对应端元所占的混合比例，所以需要服从以下2个约束条件：

其中，${\mathrm{1}}_n^{\mathrm{T}}$和${\mathrm{1}}_N^{\mathrm{T}}$分别表示长度为$n$和$N$的$\mathrm{1}$向量，式（3）表示丰度非负约束（Abundance Nonnegative Constraint， ANC），式（4）表示丰度和为一约束（Abundance Sum-to-one Constraint， ASC）。

2.2   非负矩阵分解

由于NMF具有的良好特性，NMF在高光谱解混研究上体现出强大的潜力。NMF旨在将一个非负矩阵分解为两个非负低秩矩阵，应用在高光谱解混领域时，目标就是将高光谱图像$\mathit{Y}$分解为端元矩阵$\mathit{E}$和丰度矩阵$\mathit{A}$，使得这两个矩阵的乘积逼近高光谱图像：

为衡量分解的效果，基于NMF的目标函数表示为：

其中，${‖\cdot ‖}_{\mathrm{F}}$表示Frobenius范数。针对式（6）的最优化问题是非凸的，但单对于$\mathit{E}$和$\mathit{A}$的两个子问题是凸的。基于此利用交替迭代的方法，结合梯度下降法^［19］，得到$\mathit{E}$和$\mathit{A}$更新规则：

其中，“$.\mathrm{*}$”表示逐元素乘法，“$./$”表示逐元素除法。然而，标准的NMF对噪声和算法数值初始化的非常敏感，因此，在将NMF应用于高光谱解混时，应该考虑更多的约束。

2.3   基于双权重约束的NMF模型

基于双权重约束的NMF模型构建空间权重和光谱权重共同约束丰度，目标函数为：

其中，${‖\mathit{A}‖}_{\mathrm{1,1}}={{\sum }_{j=\mathrm{1}}^N‖{\mathit{a}}_j‖}_{\mathrm{1}}$，${\mathit{a}}_j$为丰度矩阵$\mathit{A}$的第$j$列，$\odot$表示哈达玛积，${\lambda }_{\mathrm{1}}>\mathrm{0}$表示正则化参数。${\mathit{W}}_{\mathrm{s}\mathrm{p}\mathrm{e}}\in {\mathbf{R}}^{n\times n}$为光谱权重矩阵，定义为：

其中，${\mathit{A}}_{i,:}^{(k)}$表示第$k$次迭代的丰度矩阵的第$i$行，$\epsilon$是避免数值不稳定的小常数。引入光谱权重矩阵作用于丰度，在L₁范数约束下促进丰度矩阵的行稀疏性。另外，考虑到空间信息对于NMF解混的重要性，并且由于高光谱图像通常在相邻像元之间表现出较高的空间相关性，因此丰度图具有分段平滑性。基于此，第$k+\mathrm{1}$次迭代的空间权重$w_{\mathrm{s}\mathrm{p}\mathrm{a};i,j}^{(k+\mathrm{1})}$表述为：

其中，$\mathrm{𝒩}(a_{ij})$表示丰度矩阵第$i$行第$j$列元素$a_{ij}(i=\mathrm{1},\cdots ,n,j=\mathrm{1},\cdots ,N)$的邻域集合，$f(\cdot )$是表征空间相关性的函数，表示为：

其中，$\theta (a_{ij},a_{i\mathrm{ℳ}})$表示$a_{ij}$和$a_{i\mathrm{ℳ}}$的邻域显著度。若高光谱图像空间尺寸为$r\times c$，$a_{ij}$和$a_{i\mathrm{ℳ}}$对应像元的空间坐标分别为$(x,y)$和$(z,k)$，有$j=c\times (x-\mathrm{1})+y$和$\mathrm{ℳ}=c\times (z-\mathrm{1})+k$。则显著度可以定义为：

显然，式（13）表示中心元素$a_{ij}$与其邻域元素$a_{i\mathrm{ℳ}}$欧氏距离的倒数。对邻域元素来说，距离中心元素越近，显著性越大，否则，显著性就越小。

3.   基于自适应空谱约束的加权残差NMF模型

3.1   ASSC-WRNMF模型

为减轻噪声的影响，提高鲁棒性，将加权残差因子引入到标准NMF中，式（9）改写为：

其中，$\mathit{W}\in {\mathbf{R}}^{L\times L}$是作用于损失函数的对角矩阵。其对角权重定义为：

其中，${\mathit{R}}^{(k)}=\mathit{Y}-{\mathit{E}}^{(k)}{\mathit{A}}^{(k)}$，表示第$k$次迭代的残差，${\mathit{R}}_{i,:}$表示$\mathit{R}$的第$i$行，$\mu$是表征残差范数指数衰减程度的常数。由于噪声的随机性，高光谱图像每个波段受到的干扰是不同的，因此迭代过程中的残差能够反映出受噪声影响的程度。通过迭代时产生的残差为损失函数每一行分配权重，对残差大的行分配较小的权重，残差小的行分配较大的权重，随着算法迭代来调整数据的拟合效果，从而减轻在优化过程中噪声的影响。

此外，式（11）中邻域的选择对解混结果至关重要，常用的选择方法是使用固定形状的窗口，如8连接邻域^［21］等。这种方式复杂度较低，操作简单，但由于高光谱图像地物的复杂性，图像通常存在大量的边缘和地物过渡区域。在处理这些区域时，固定邻域窗口的处理效果受相关性较小的像元影响较大，限制了解混的性能。为解决该问题，本文结合丰富的空间结构信息，提出一种利用像元相似性来确定邻域的方法。

通常来说，像元间的相似性通过两像元光谱曲线的相似程度来衡量，由于高光谱图像在相邻像元间往往高度相关，因此将像元间的空间距离纳入到像元相似性度量上。综上，本文提出像元空谱相似度来衡量像元相似性，其数值由像元的光谱差异和空间距离共同确定。假定高光谱图像$\mathit{Y}$的第$a$个和第$b$个像元分别为${\mathit{y}}_a$和${\mathit{y}}_b$，则像元空谱相似度定义为：

其中，${\sigma }_{\mathrm{1}}$是控制像元光谱相似性的参数，$d({\mathit{y}}_a,{\mathit{y}}_b)$表示两像元间的空间欧式距离，${\sigma }_{\mathrm{2}}$是控制距离显著性的参数。显然，两像元光谱差异越小，空间距离越近，空谱相似度越大。由于丰度的列向量表示一个像元中地物的所占比例，并且相似像元的丰度也相似，因此同一列丰度元素的邻域空间坐标是一样的。基于以上分析，根据式（16），对于空间尺寸为$r\times c$的高光谱图像，其丰度矩阵第$j$列向量${\mathit{a}}_{:j}$对应的像元空谱相似度矩阵${\mathit{H}}^j\in {\mathbf{R}}^{r\times c}$中第$X$行第$Y$列元素定义为：

此外，如何确定邻域数量是另一个重要的问题。由于地物的复杂性，若邻域数量采用固定值，在处理某些场景时，性能会受到限制。并且像元空谱相似度差距较大，显著的值集中在一个小区域中。基于此，本文通过设定阈值的方法来确定邻域数量。由此，${\mathit{a}}_{:j}$对应邻域的空间坐标族${\varphi }_a^j$：

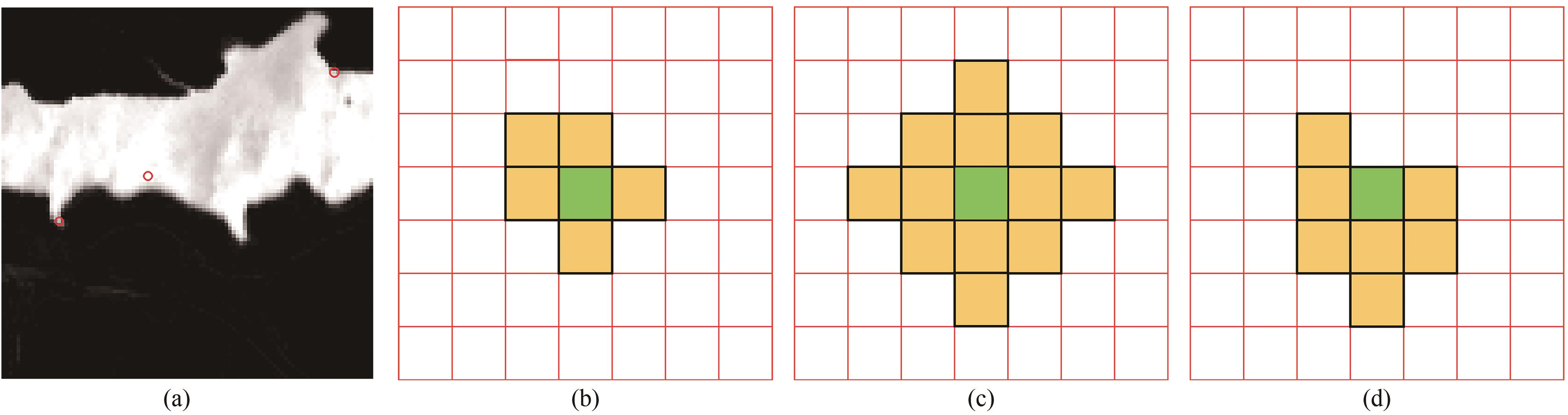
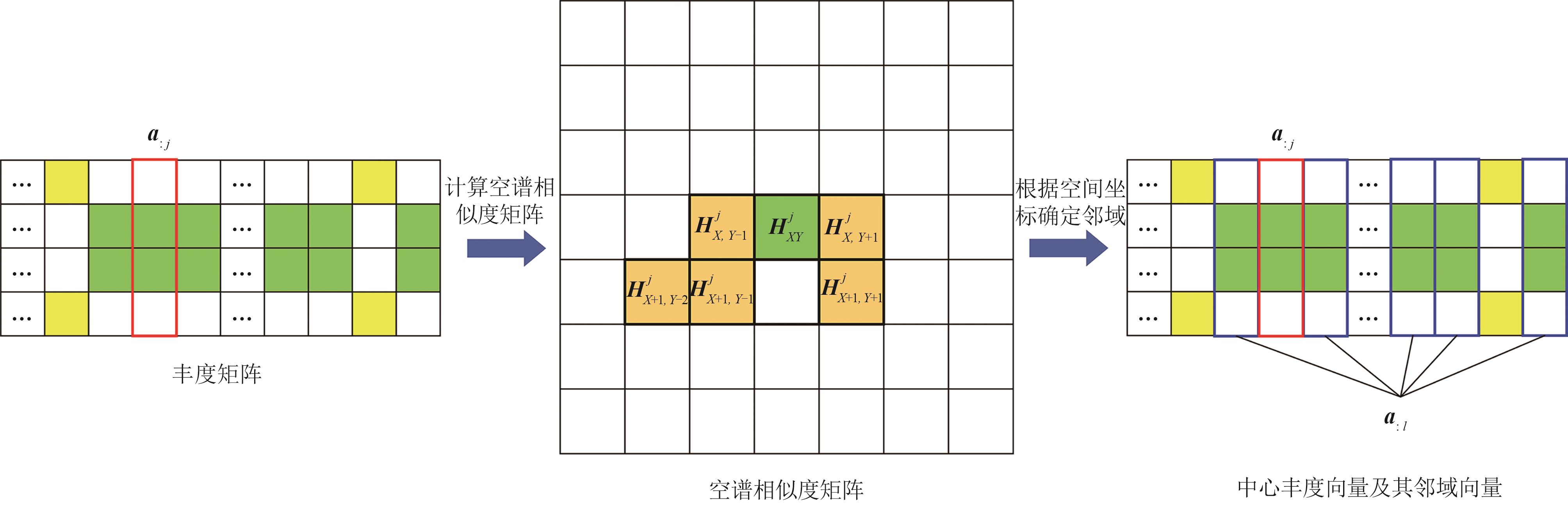
其中，$\mathrm{m}\mathrm{a}\mathrm{x}({\mathit{H}}^j)$是矩阵${\mathit{H}}^j$的最大元素值，$T\in (\mathrm{0,1})$表示确定邻域数量的阈值倍数。由式（18）设置${\mathit{H}}^j$最大元素值的$T$倍为阈值，把大于该阈值的元素的坐标记为${\mathit{a}}_{:j}$的邻域空间坐标。由此，$a_{ij}$的邻域集合$\mathrm{𝒩}(a_{ij})$可以表示为：

图1展示了通过像元空谱相似度确定邻域的过程。图中${\mathit{a}}_{:j}$表示丰度矩阵的第$j$列，计算${\mathit{a}}_{:j}$对应像元的空谱相似度矩阵，矩阵中绿色背景代表中心元素，黄色背景代表邻域元素，将邻域元素的空间坐标映射到丰度矩阵中，即得到了${\mathit{a}}_{:j}$的邻域向量${\mathit{a}}_{:l}$。

图  1  自适应邻域确定过程

Fig.  1.  Adaptive neighborhood determination process

下载: 全尺寸图片 幻灯片

图2展示了在某场景下自适应邻域选择的结果。图2（a）是该场景某一地物的丰度灰度图，其中红色圆框处的丰度邻域从左往右分别由图2（b）、图2（c）和图2（d）所示。从图2（b）和图2（d）中可以看到在图像边缘区域所提的自适应策略能够针对性地确定邻域，并规避相似性小的像元丰度。图2（c）展示了在像元光谱差异不大的区域的邻域，此时空间距离成为确定邻域的主要因素，邻域数量较边缘区域更多。

图  2  自适应邻域选择示意图，（a）中红框处的邻域从左到右分别是（b）、（c）和（d）

Fig.  2.  Schematic of adaptive neighborhood selection； from left to right， the neighborhoods at the red boxes in （a） are （b）， （c）， and （d）， respectively

下载: 全尺寸图片 幻灯片

在此基础上，针对高光谱图像端元光谱分段平滑的特性，提出了一种端元平滑约束策略。通过无约束的NMF得到估计端元矩阵${\mathit{E}}_{\mathrm{e}\mathrm{s}\mathrm{t}}$，将其作为先验信息来确定端元光谱的平滑等级。并由${\mathit{E}}_{\mathrm{e}\mathrm{s}\mathrm{t}}$中端元光谱的连续三个反射值来共同度量端元光谱的平滑等级参数，其中平滑等级参数由权重矩阵$\mathit{Q}$描述，定义为：

其中，$i=\mathrm{1},\cdots ,L-\mathrm{2}$，$j=\mathrm{1},\cdots ,n$，${\mathit{E}}_{\mathrm{e}\mathrm{s}\mathrm{t};i,j}$表示估计端元矩阵${\mathit{E}}_{\mathrm{e}\mathrm{s}\mathrm{t}}$的第$i$行第$j$列元素，$\eta$是控制平滑程度的参数。式中端元平滑等级参数${\mathit{Q}}_{ij}$由估计光谱与其前后两个反射值均值之差来度量，${\mathit{E}}_{\mathrm{e}\mathrm{s}\mathrm{t};i+\mathrm{1},j}$越接近$({\mathit{E}}_{\mathrm{e}\mathrm{s}\mathrm{t};i+\mathrm{2},j}+{\mathit{E}}_{\mathrm{e}\mathrm{s}\mathrm{t};i,j})/\mathrm{2}$，该处越平滑，权重${\mathit{Q}}_{ij}$就越大。综上，端元平滑约束项写为：

通过对端元光谱$\mathit{E}$分配权重${\mathit{Q}}_{ij}$，对突变较大的反射值分配小权重，对平滑变化的反射值分配大权重，有效调整在迭代过程中端元光谱的平滑程度。

综上，本文提出的ASSC-WRNMF模型的最终目标函数写作：

其中，${\lambda }_{\mathrm{1}},{\lambda }_{\mathrm{2}}>\mathrm{0}$表示正则化参数。

3.2   模型优化

针对式（22）的优化，与标准NMF类似，对于$\mathit{E}$和$\mathit{{\rm A}}$来说不是凸的，因此同时优化$\mathit{E}$和$\mathit{{\rm A}}$非常困难。为了解决这一问题，将其分为两个凸的子问题：

优化策略包含两个阶段：端元估计和丰度估计。在每一步中，待更新变量的值根据其他变量的当前估计值进行更新，从而使目标函数的值迭代减小。算法具体步骤如下。

（1）端元矩阵估计：端元矩阵$\mathit{E}$的优化问题由下式给出：

其中，$\mathrm{T}\mathrm{r}(\cdot )$表示矩阵的迹，$\Psi \in {\mathbf{R}}^{L\times n}$是拉格朗日乘子。求解该问题，需要求方程对$\mathit{E}$的偏导，结合KKT条件得到以下方程：

在式（26）两侧同时点乘矩阵$\mathit{E}$，并结合式（27）可得$\mathit{E}$的更新公式为：

其中，$\frac{\partial F_{\mathrm{1}}(\mathit{E})}{\partial \mathit{E}}$是$F_{\mathrm{1}}(\mathit{E})$对$\mathit{E}$的偏导，记为$\mathit{M}$，则其元素${\mathit{M}}_{ij}$表示为：

其中$j=\mathrm{1},\cdots ,n$。

（2）丰度矩阵估计：对于丰度矩阵$\mathit{A}$的优化问题，采用文献［6］提出的策略，将ASC隐式地包含在目标式中。通过高光谱图像矩阵和端元矩阵的增广形式代替原矩阵，写作：

其中，$\delta$用于控制ASC的影响程度，值越大，丰度和越接近1。替换后，丰度矩阵$\mathit{A}$的优化问题由下式给出：

其中，$\tilde{\mathit{W}}$是$\mathit{W}$的增广形式，其对角元素为：

其中，参数$\beta$同样用于控制ASC的影响程度。针对式（31）的优化问题，由KKT条件下得到如下方程：

相似地，在式（33）两侧同时点乘矩阵$\mathit{A}$，并结合式（34）可得丰度矩阵$\mathit{A}$的更新公式：

3.3   算法实现

由于ASSC-WRNMF算法基于NMF模型，故仍然具有全局非凸性，所以初始值的选取尤为重要。端元矩阵$\mathit{E}$和丰度矩阵$\mathit{A}$的初始化通常有两种方法：第一种是在区间$[\mathrm{0,1}]$的取值范围内随机初始化矩阵$\mathit{E}$和$\mathit{A}$的值，并对$\mathit{A}$的每一列进行归一化，以满足ASC。第二种方法就是利用顶点成分分析（Vertex Component Analysis， VCA）和全约束最小二乘法（Fully Constrained Least Squares， FCLS）分别对$\mathit{E}$和$\mathit{A}$初始化。考虑到NMF模型对初始化较为敏感，为保证算法性能和收敛速度，在本文的所有实验中均使用VCA-FCLS算法来进行初始化。

此外，对于端元平滑正则化参数${\lambda }_{\mathrm{2}}$，通过估计端元光谱的总体平滑程度自适应调整，表示为：

其中，$\overline{Q^{\text{'}}}$表示端元平滑权重矩阵$\mathit{Q}$的归一化矩阵${\mathit{Q}}^{\text{'}}$的均值，${\mathit{Q}}^{\text{'}}$中元素定义为${\mathit{Q}}_{ij}^{\text{'}}=({\mathit{Q}}_{ij}-\mathrm{m}\mathrm{i}\mathrm{n}(\mathit{Q}))/(\mathrm{m}\mathrm{a}\mathrm{x}(\mathit{Q})-$$\mathrm{m}\mathrm{i}\mathrm{n}(\mathit{Q}))$。另外，参考文献［6］，设置ASC参数$\delta$为15。

对于算法迭代的停止条件，采用常用的两个迭代停止准测。第一种是设置最大迭代次数，当迭代次数达到设置的值时则停止迭代并输出结果，对于ASSC-WRNMF算法最大迭代次数的确定将在4.1.1节进行讨论。第二种就是当前迭代与上一次迭代目标函数，即式（22）的数值之差的绝对值小于一定阈值时迭代停止，即

为保证算法迭代效果，根据经验设置算法停止阈值$\mathrm{T}\mathrm{O}\mathrm{L}$为$\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$。综上所述，ASSC-WRNMF算法的整体流程如表1所示。

表  1  ASSC-WRNMF算法流程

Tab.  1.  ASSC-WRNMF algorithm process

输入：高光谱矩阵$\mathit{Y}$，端元数量$n$。
输出：更新后的端元矩阵$\mathit{E}$和丰度矩阵$\mathit{A}$。
步骤1：通过VCA-FCLS算法初始化端元矩阵$\mathit{E}$和丰度矩阵$\mathit{A}$；
步骤2：根据式(20)计算端元平滑权重矩阵$\mathit{Q}$；
步骤3：根据式(18)计算并存储每个丰度列向量对应的空间邻域坐标族；
步骤4：根据式(15)计算迭代后的残差权重对角矩阵$\mathit{W}$；
步骤5：通过式(10)和(11)分别更新光谱加权矩阵${\mathit{W}}_{\mathrm{s}\mathrm{p}\mathrm{e}}$和空间加权矩阵${\mathit{W}}_{\mathrm{s}\mathrm{p}\mathrm{a}}$；
步骤6：根据式(28)更新端元矩阵$\mathit{E}$；
步骤7：根据式(30)和(32)分别增广$\mathit{Y}$、$\mathit{E}$和$\mathit{W}$得到${\displaystyle \tilde{\mathit{Y}}}$、${\displaystyle \tilde{\mathit{E}}}$和${\displaystyle \tilde{\mathit{W}}}$；
步骤8：根据式(35)更新丰度矩阵$\mathit{A}$；
步骤9：如果达到最大迭代次数或者满足停止迭代条件，则输出$\mathit{E}$和$\mathit{A}$，否则返回步骤4。

下载: 导出CSV 

| 显示表格

4.   实验结果与分析

本文的实验分别在模拟数据集和真实数据集上进行，为评估ASSC-WRNMF算法的解混效果，将其与SSWNMF^［21］、L₂₁SSR-NMF^［20］、WRNMF^［6］、RONMF^［16］、SGNMF^［18］和L_1/2-NMF^［14］对比。对于所有实验，本文采用光谱角距离（Spectral Angle Distance， SAD）和均方根误差（Root Mean Square Error， RMSE）两个精度指标来比较各算法的解混性能。光谱向量$\mathit{a}$和$\mathit{b}$的SAD定义为：

通过计算SAD来衡量估计光谱和真实光谱间的差异程度。RMSE则是度量真实地物丰度向量$\mathit{c}$和算法反演的丰度向量$\stackrel{̑}{\mathit{c}}$之间的差异程度，表示为：

其中，$N$表示像元数量。对于SAD和RMSE，两者数值越小说明端元估计越完备，丰度反演结果越好，算法性能越好。

4.1   模拟数据实验

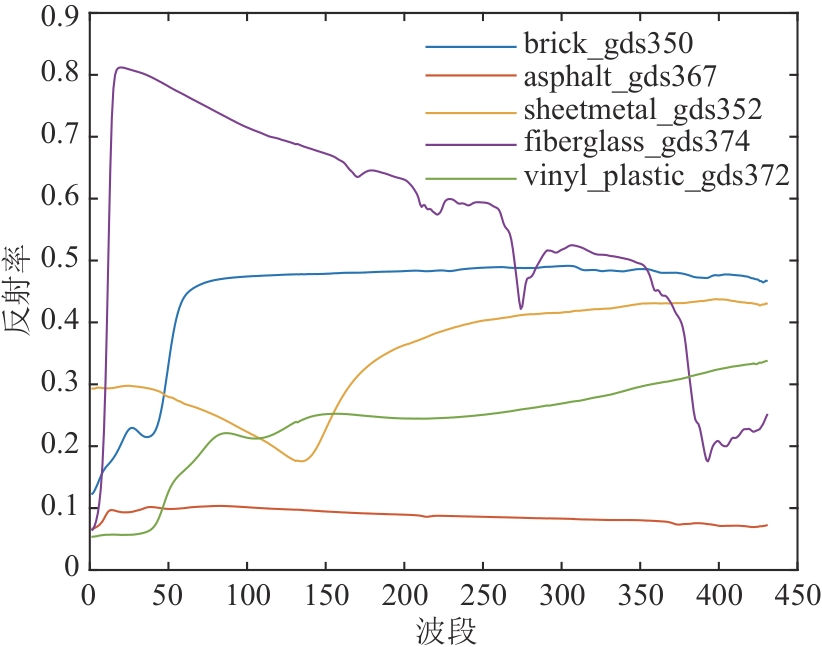
模拟数据实验部分选取USGS光谱库中的5个光谱作为端元，包含431个波段，丰度图在满足ANC和ASC的前提下随机生成，具有分段平滑区域，包含$\mathrm{128}\times \mathrm{128}$个像元。图3显示了5个端元的光谱曲线。此外，由于高光谱图像在采集过程中通常会受到噪声污染，为模拟该过程，在实验中对模拟数据添加不同等级信噪比（Signal-Noise Ratio， SNR）的噪声。为确保算法的有效性，所有实验在相同的参数和环境下重复50次，最终结果取均值。

图  3  模拟数据端元光谱曲线

Fig.  3.  Simulated data endmembers spectral curve

下载: 全尺寸图片 幻灯片

4.1.1   参数选择

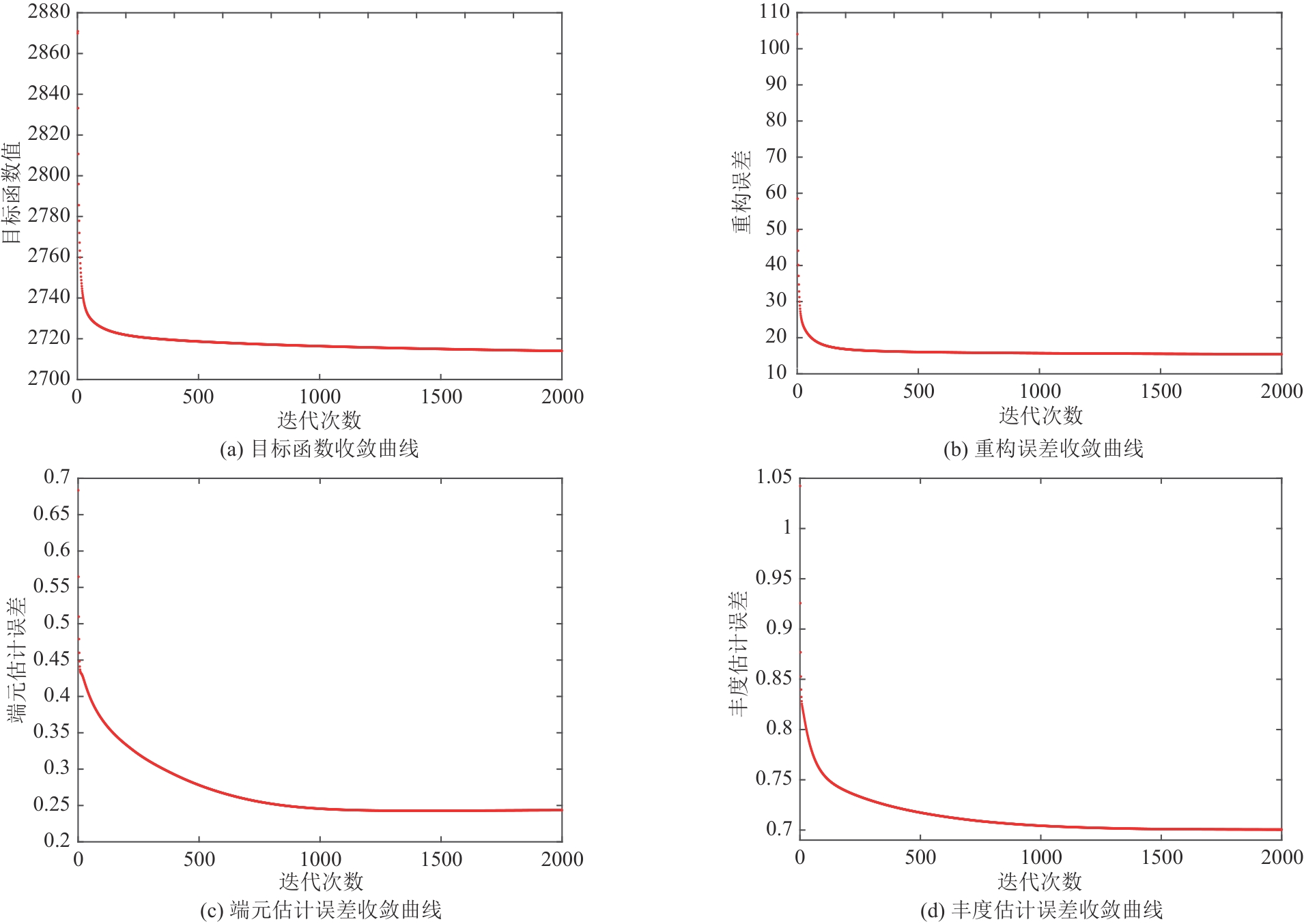
本文提出的ASSC-WRNMF算法需要手动确定最大迭代次数、残差范数指数衰减参数$\mu$、空谱正则化参数${\lambda }_{\mathrm{1}}$和邻域阈值倍数$T$三个参数的数值。在确定各参数之前，需要对收敛性进行分析。参考文献［19］中的收敛性分析和证明方法，本实验通过绘制收敛曲线来说明所提算法的收敛性。图4展示了ASSC-WRNMF算法在SNR=25 dB时在模拟数据上的收敛效果，图中横轴表示迭代次数，（a）、（b）、（c）和（d）的纵轴分别表示目标函数值、重构误差、端元估计误差和丰度估计误差。如图4（a）和（b）所示，目标函数值和重构误差随着迭代次数的增加快速减小，在200次后曲线趋于平稳，图4（c）和（d）中端元和丰度的估计误差不断减小且在1000次迭代收敛至平稳值。因此，为保证算法收敛效果和运行速度，设置最大迭代次数为1000。

图  4  ASSC-WRNMF算法收敛曲线

Fig.  4.  Convergence curve of the ASSC-WRNMF algorithm

下载: 全尺寸图片 幻灯片

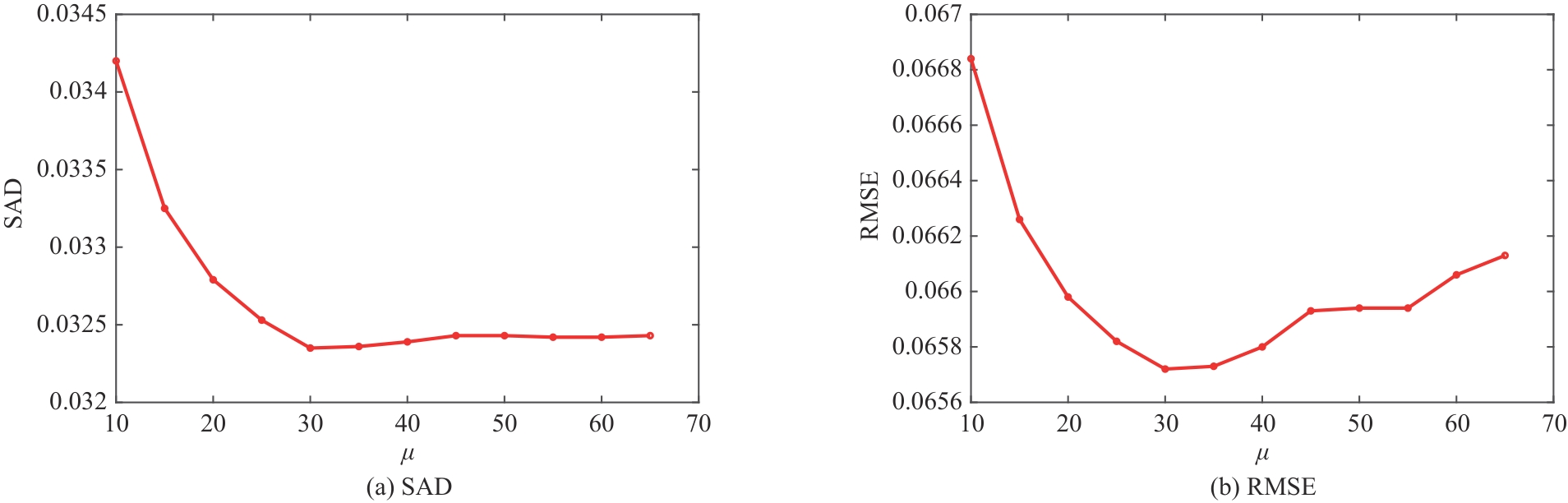
针对参数$\mu$，本实验将从｛10，15，20，25，30，35，40，45，50，55，60，65｝中取值，研究参数$\mu$的不同取值对算法性能的影响。图5展示了ASSC-WRNMF算法在模拟数据集中RMSE和SAD在随$\mu$的变化曲线，从图中可以看出当$\mu$从10增加到30时SAD和RMSE迅速降低，随后在30到65变化过程中SAD缓慢增加并趋于平缓，RMSE逐渐增大。由此可见当$\mu$取值为30时，SAD和RMSE的值最小，性能最佳。基于以上实验结果分析，参数$\mu$设置为30。

图  5  ASSC-WRNMF相对于参数$\mu$的性能变化

Fig.  5.  Performance changes of ASSC-WRNMF， relative to the parameter $\mu$

下载: 全尺寸图片 幻灯片

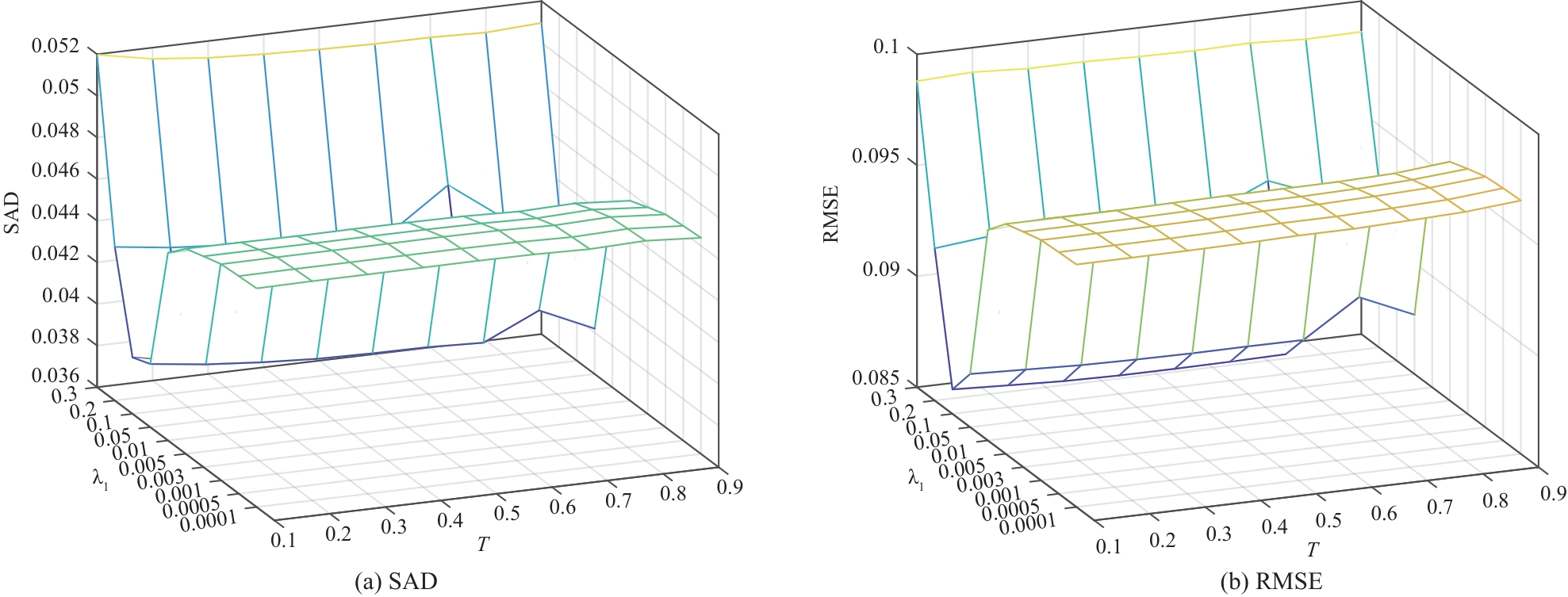
此外对于参数${\lambda }_{\mathrm{1}}$和$T$，在相同实验环境下研究这两个参数在不同取值下对算法性能的影响。${\lambda }_{\mathrm{1}}$从｛0.0001，0.0005，0.001，0.003，0.005，0.01，0.05，0.1，0.2，0.3｝中取值，$T$从｛0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9｝中取值。参考文献［6］和［24］的研究，设置$\mu =\mathrm{20}$，$\epsilon =\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}$，$\sigma =\mathrm{1}$，$\eta =\mathrm{1}$，$\beta =\mathrm{0.5}$。图6展示了ASSC-WRNMF算法在模拟数据集中相对于参数${\lambda }_{\mathrm{1}}$和$T$的性能表现，（a）和（b）分别表示SAD和RMSE的变化趋势。从图6（a）和（b）中可以看出，当${\lambda }_{\mathrm{1}}$在0.3到0.1区间时，SAD和RMSE随${\lambda }_{\mathrm{1}}$的减小而大幅减小，在0.1到0.0001区间时，两者随${\lambda }_{\mathrm{1}}$的减小在突然上升之后趋于平缓，说明在${\lambda }_{\mathrm{1}}=\mathrm{0.1}$时，自适应空谱约束能够发挥最佳的作用。并且在${\lambda }_{\mathrm{1}}=\mathrm{0.1}$时，SAD和RMSE随$T$的增加逐渐减小并在$T=\mathrm{0.7}$时到达最小值，随后上升，表明当$T$偏大时，邻域数量大幅减少，导致丰度平滑约束性能下降。因此，${\lambda }_{\mathrm{1}}$和$T$的最佳值分别为0.1和0.7。基于以上分析，在其余实验中本文设定${\lambda }_{\mathrm{1}}=\mathrm{0.1}$，$T=\mathrm{0.7}$。

图  6  ASSC-WRNMF相对于参数${\lambda }_{\mathrm{1}}$和$T$的性能变化

Fig.  6.  Performance changes of ASSC-WRNMF， relative to the parameters ${\lambda }_{\mathrm{1}}$ and $T$

下载: 全尺寸图片 幻灯片

4.1.2   性能分析

本实验中，对模拟数据添加了20、30、40、50 dB四个等级信噪比的高斯噪声。表2和表3分别展示了各种算法在不同等级噪声干扰下的SAD和RMSE结果，表中粗体表示最优结果。从表2和表3可以看出，在不同等级噪声影响下，ASSC-WRNMF算法相较于其他算法能获得更低的SAD和RMSE值，表明本文算法提取的端元光谱精度最高，反演的丰度最接近真实丰度。相较于RONMF，本文算法的SAD更低，这表明所提的端元平滑约束与端元独立性约束相比更具优势。并且与大多仅结合丰度稀疏或者平滑约束的算法相比，将丰度稀疏和平滑约束相融合的ASSC-WRNMF能够获得更好的性能，表明该策略的有效性。此外，对比SSWNMF和WRNMF算法，ASSC-WRNMF通过加权残差因子改进NMF模型，并且利用像元的光谱和空间信息确定丰度邻域构造自适应空谱约束，使ASSC-WRNMF的解混性能更好。在强噪声干扰下，本文算法仍然能够取得最佳的性能，足以说明本文算法具有明显的优势以及较强的鲁棒性。

表  2  各算法在不同SNR下的SAD对比

Tab.  2.  Comparison of the SAD values of various algorithms under different SNRs

SNR/dB	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
20	0.0796$\pm$0.52%	0.0337$\pm$0.41%	0.0347$\pm$0.40%	0.0352$\pm$0.42%	0.0370±0.42%	0.0344±0.46%	0.0333$\pm$0.43%
30	0.0340$\pm$0.14%	0.0369$\pm$0.18%	0.0344$\pm$0.20%	0.0327$\pm$0.18%	0.0319$\pm$0.20%	0.0326$\pm$0.18%	0.0315$\pm$0.19%
40	0.0402$\pm$0.09%	0.0428$\pm$0.14%	0.0435$\pm$0.20%	0.0384$\pm$0.15%	0.0377$\pm$0.20%	0.0384$\pm$0.16%	0.0372$\pm$0.14%
50	0.0413$\pm$0.17%	0.0440$\pm$0.21%	0.0441$\pm$0.23%	0.0393$\pm$0.10%	0.0376$\pm$0.18%	0.0394$\pm$0.16%	0.0381$\pm$0.15%

下载: 导出CSV 

| 显示表格

表  3  各算法在不同SNR下的RMSE对比

Tab.  3.  Comparison of the RMSE values of various algorithms under different SNRs

SNR/dB	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
20	0.1335$\pm$0.28%	0.1153$\pm$0.25%	0.1111$\pm$0.26%	0.1117$\pm$0.25%	0.1101$\pm$0.30%	0.1123$\pm$0.25%	0.1085$\pm$0.25%
30	0.0534$\pm$0.19%	0.0559$\pm$0.25%	0.0577$\pm$0.31%	0.0529$\pm$0.26%	0.0525$\pm$0.25%	0.0529$\pm$0.26%	0.0521$\pm$0.25%
40	0.0538$\pm$0.29%	0.0577$\pm$0.36%	0.0565$\pm$0.33%	0.0504$\pm$0.39%	0.0506$\pm$0.33%	0.0510$\pm$0.37%	0.0484$\pm$0.37%
50	0.0560$\pm$0.20%	0.0598$\pm$0.23%	0.0585$\pm$0.28%	0.0524$\pm$0.20%	0.0517$\pm$0.19%	0.0529$\pm$0.23%	0.0503$\pm$0.19%

下载: 导出CSV 

| 显示表格

4.2   真实数据实验

在本节中，采用两个真实高光谱数据集进行实验。第一个是高光谱解混实验常用的JasperRidge场景，第二个是由高光谱数字采集实验（HYDICE）获得的Urban场景。与模拟数据实验一样，所有的结果是由50次重复实验后取均值得到。

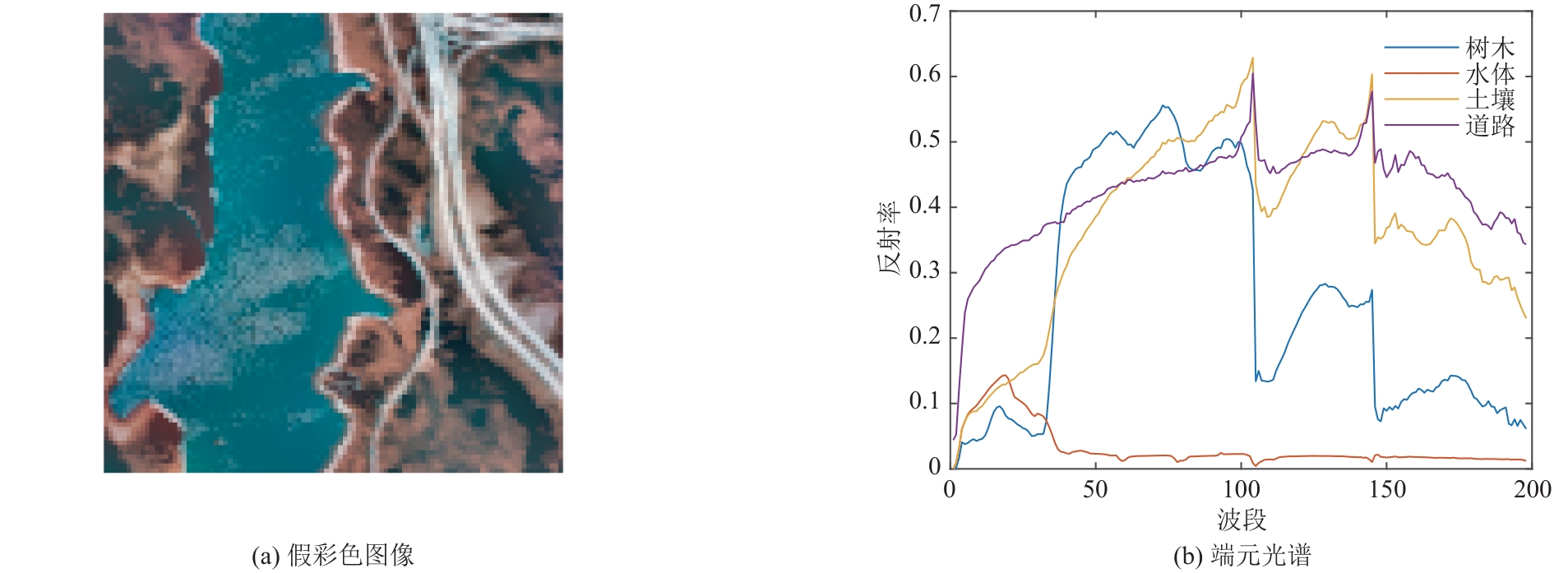
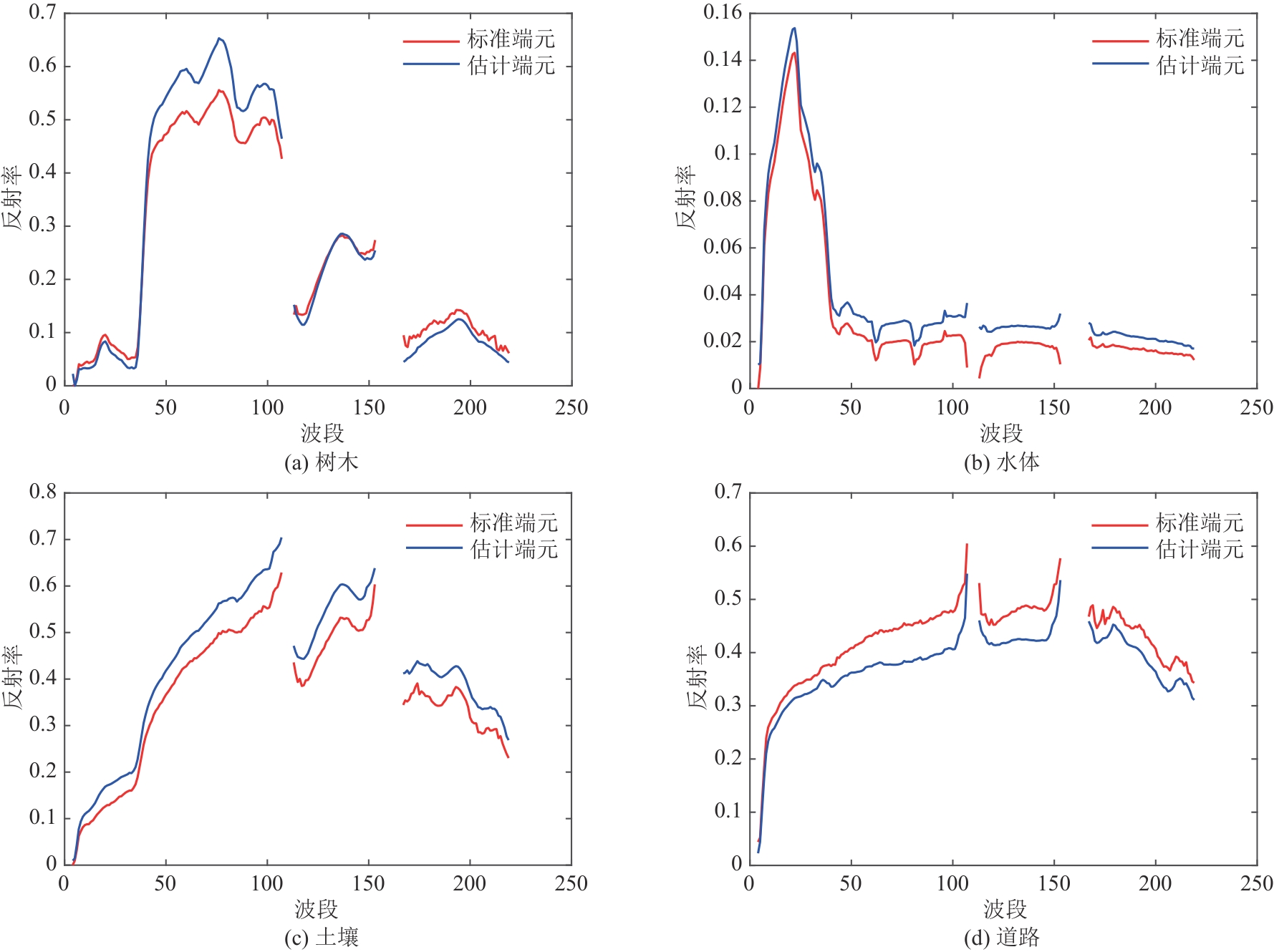
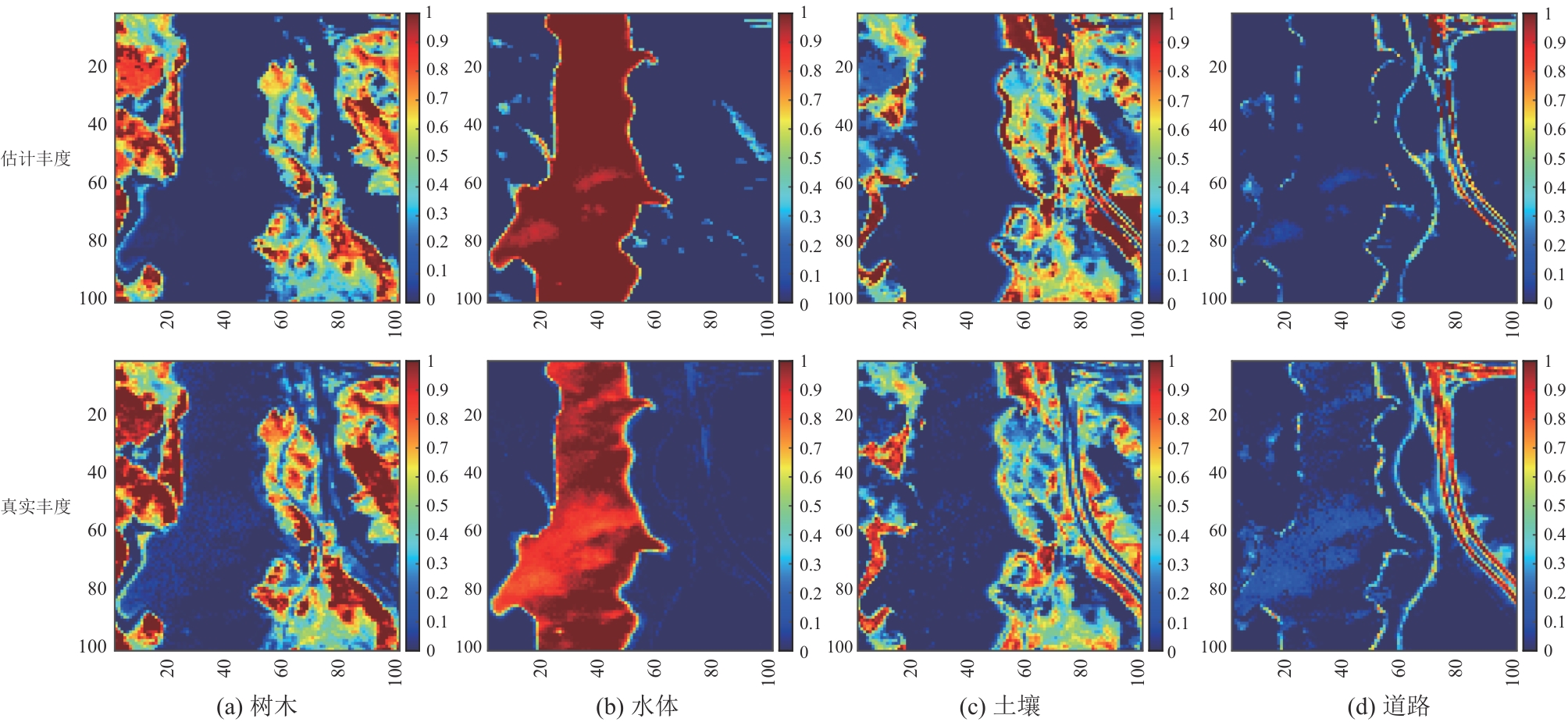
（1）JasperRidge数据集包含224个波段，覆盖波长范围380~2500 nm，含有100$\times$100个像元。为保证实验的准确性，去除受浓密的水蒸气和大气影响的1~3、108~112、154~166和220~224波段后，剩余198个波段。此数据集共有4个端元地物，分别是道路、土壤、水体和树木。JasperRidge场景的假彩色图像和4个端元的光谱如图7所示。

图  7  JasperRidge场景和对应端元光谱曲线

Fig.  7.  JasperRidge scene and corresponding endmembers spectral curves

下载: 全尺寸图片 幻灯片

表4给出了各算法在JasperRidge数据集下的SAD对比，包含每个端元地物的SAD和总体均值，最优实验结果由粗体表示。从表4可以看出，ASSC-WRNMF在SAD方面取得了非常不错的性能，在树木、土壤和道路三个端元上，ASSC-WRNMF的SAD明显低于其他算法，并且在总体均值上获得了最佳的性能，这表明了所提出的端元平滑约束应用于改进NMF解混的有效性。表5比较了各算法在该数据集下的RMSE和运行时间，可以看出在利用空间信息的方法中，所提出的ASSC-WRNMF比SSWNMF、L₂₁NMF-SSR、WRNMF和SGNMF能够获得更低的RMSE并且运行速度更快，充分表明了自适应空谱约束相较于其他结合空间信息的丰度约束有明显的优势。图8展示了通过ASSC-WRNMF算法获得的估计端元光谱与真实端元光谱的对比，从图中可以看出估计端元与真实端元的差距较小，保持一致性和高度相关性。此外，图9显示了ASSC-WRNMF算法估计的4个端元对应丰度和真实丰度的对比，可以看出ASSC-WRNMF获得的丰度图与真实丰度图非常吻合。从性能对比和端元及丰度的估计值与真实值的对比，足以说明ASSC-WRNMF算法在JasperRidge数据集上具有更好的解混性能。

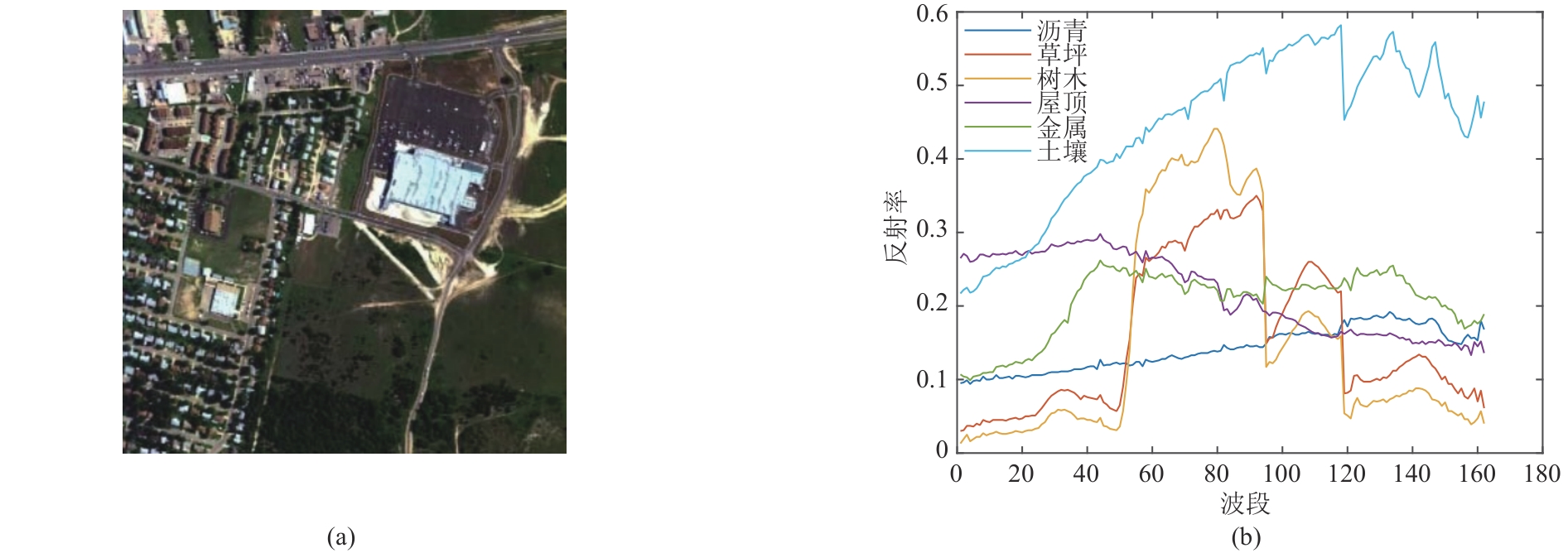
表  4  各算法在JasperRidge数据集上的SAD对比

Tab.  4.  Comparison of the SAD values of various algorithms on the JasperRidge dataset

	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
树木	0.0542$\pm$0.77%	0.0515$\pm$0.83%	0.0634$\pm$0.80%	0.0580$\pm$0.87%	0.0549$\pm$0.75%	0.0579$\pm$0.82%	0.0474$\pm$0.81%
水体	0.2931$\pm$2.30%	0.2930$\pm$2.77%	0.2513$\pm$2.78%	0.2324$\pm$2.93%	0.2643$\pm$2.93%	0.2329$\pm$2.85%	0.2446$\pm$2.85%
土壤	0.0695$\pm$1.15%	0.0734$\pm$1.26%	0.0681$\pm$1.12%	0.0786$\pm$1.56%	0.0710$\pm$1.25%	0.0788$\pm$1.33%	0.0605$\pm$1.08%
道路	0.0615$\pm$0.73%	0.0643$\pm$0.84%	0.1225$\pm$0.87%	0.0653$\pm$0.84%	0.0663$\pm$0.79%	0.0653$\pm$0.84%	0.0584$\pm$0.76%
平均	0.1196$\pm$0.70%	0.1206$\pm$0.78%	0.1263$\pm$0.96%	0.1086$\pm$0.78%	0.1048$\pm$0.80%	0.1087$\pm$0.80%	0.1027$\pm$0.76%

下载: 导出CSV 

| 显示表格

表  5  各算法在JasperRidge数据集上的RMSE和运行时间对比

Tab.  5.  Comparison of the RMSE values and runtimes of various algorithms on the JasperRidge dataset

	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
RMSE	0.0717$\pm$0.36%	0.0632$\pm$0.36%	0.0638$\pm$0.36%	0.0645$\pm$0.40%	0.0650$\pm$0.43%	0.0652$\pm$0.34%	0.0558$\pm$0.35%
时间/s	5.3656	18.2253	3.3941	65.7308	27.3689	18.2502	11.9131

下载: 导出CSV 

| 显示表格

图  8  ASSC-WRNMF算法在JasperRidge数据集上提取的端元与真实端元的对比

Fig.  8.  Comparison between endmembers extracted by the ASSC-WRNMF algorithm and real endmembers on the JasperRidge dataset

下载: 全尺寸图片 幻灯片

图  9  ASSC-WRNMF算法在JasperRidge数据集上估计丰度与真实丰度的对比

Fig.  9.  Comparison between the abundance estimated by the ASSC-WRNMF algorithm and real abundance on the JasperRidge dataset

下载: 全尺寸图片 幻灯片

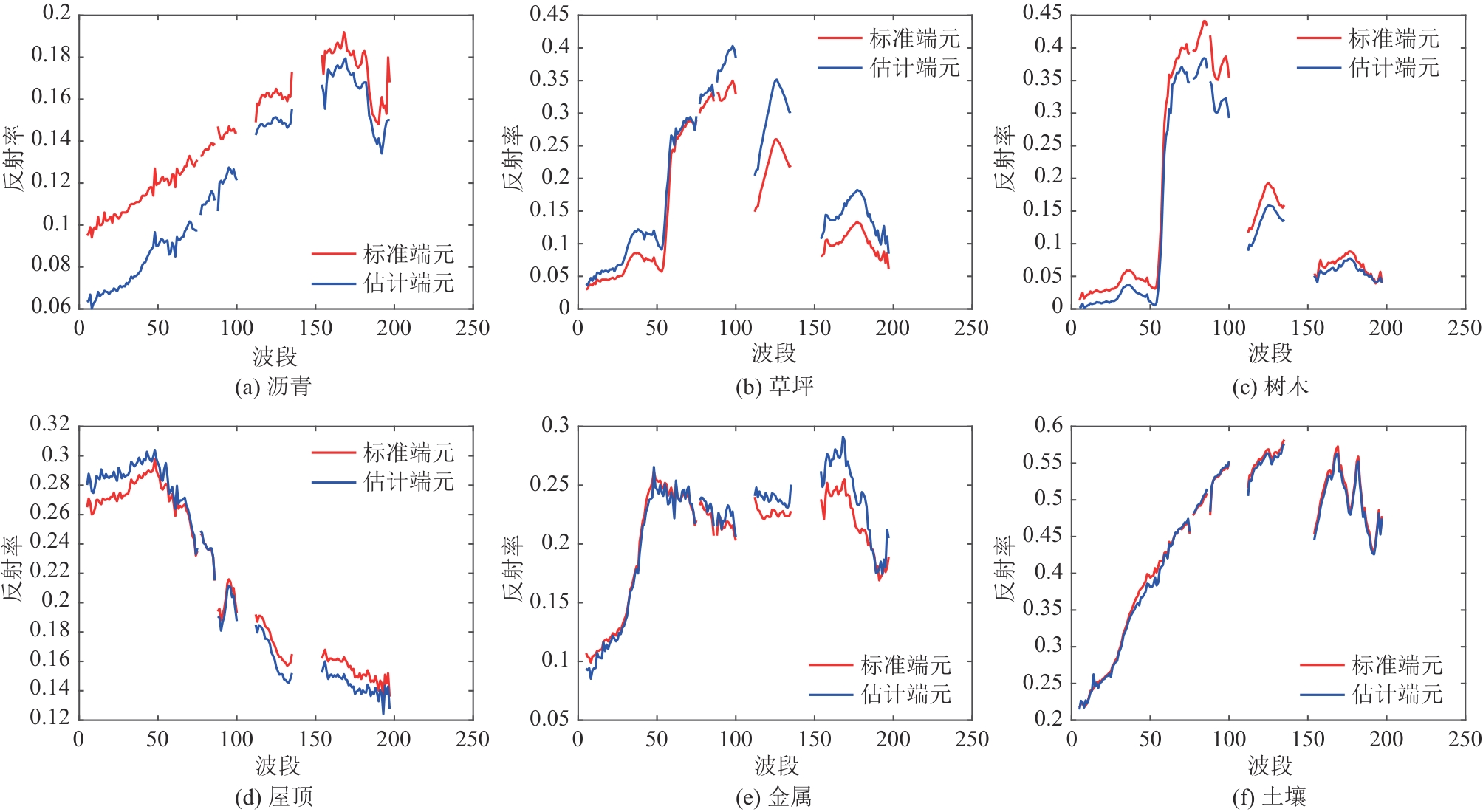
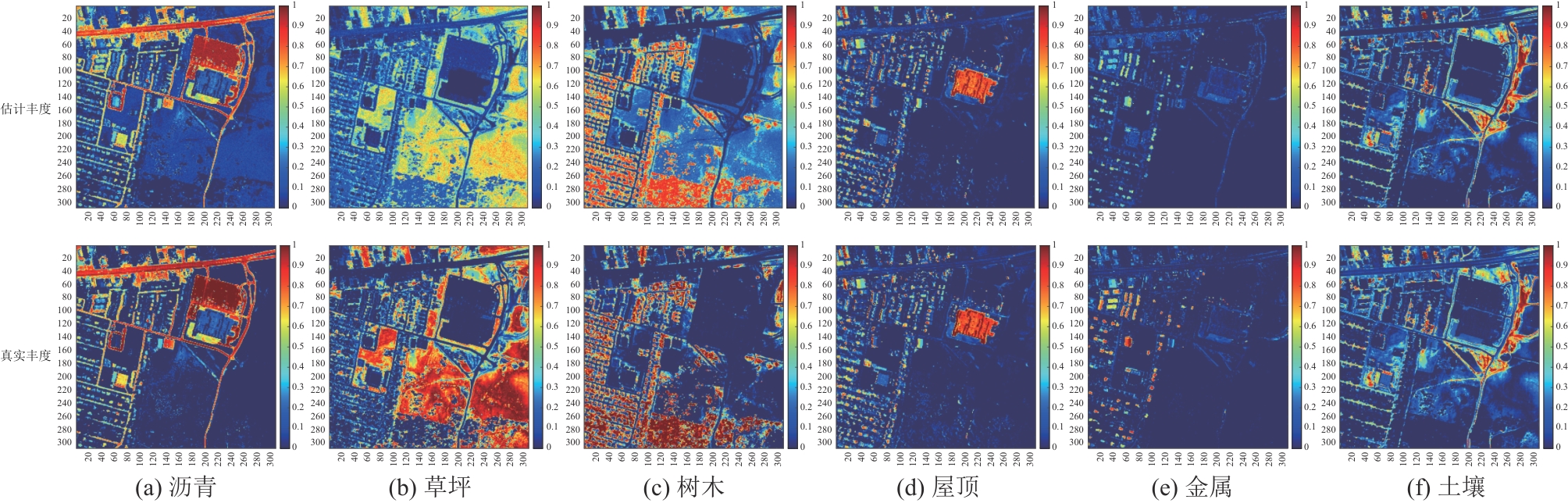
（2）Urban数据集是高光谱混合研究中使用最广泛的高光谱数据之一。该数据集共有307$\times$307个像元，210个波段，波长范围400~2500 nm。同样的，去除受浓密的水蒸气和大气影响的1~4、76、87、101~111、136~153和198~210波段后，剩余162个波段。此外，Urban数据集有三个版本的地面实况，分别包含4个、5个和6个端元。本文实验采用含6个端元的版本，分别是沥青、草坪、树木、屋顶、金属和土壤。图10展示了Urban场景的假彩色图像和6个端元的光谱曲线。

图  10  Urban场景和对应端元光谱曲线

Fig.  10.  Urban scene and corresponding endmembers spectral curves

下载: 全尺寸图片 幻灯片

表6是在Urban数据集上各算法的SAD值，最优结果用粗体表示。从表中可以看出，所提出的ASSC-WRNMF获得了最低的平均SAD，并且对于沥青、屋顶、金属和土壤四种地物，也能够获得最低的SAD。表7展示了不同算法在Urban数据集上的RMSE和运行时间。对比其他算法，ASSC-WRNMF算法的RMSE值最低，说明估计丰度图与真实丰度图之间的差异最小。此外，对比其他利用空间信息约束丰度的算法，ASSC-WRNMF的运行速度更快，说明在处理复杂的大型高光谱图像时，ASSC-WRNMF算法仍然具有优势。图11展示了ASSC-WRNMF算法估计的端元与真实端元的一致性。图12显示了ASSC-WRNMF获得的针对沥青、草坪、树木、屋顶、金属和土壤的丰度图的估计结果，可以看到ASSC-WRNMF获得的丰度图与真实丰度图非常吻合。综合以上实验结果，在Urban数据集上，ASSC-WRNMF具备出色的解混性能。

表  6  各算法在Urban数据集上的SAD对比

Tab.  6.  Comparison of the SAD values of various algorithms on the Urban dataset

	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
沥青	0.1444$\pm$0.96%	0.1028$\pm$1.00%	0.1247$\pm$0.99%	0.1270$\pm$1.07%	0.1231$\pm$1.03%	0.1364$\pm$0.98%	0.0909$\pm$1.02%
草坪	0.1718$\pm$0.85%	0.2015$\pm$0.90%	0.1972$\pm$0.94%	0.1992$\pm$0.97%	0.1901$\pm$0.88%	0.2033$\pm$0.93%	0.1986$\pm$0.90%
树木	0.1090$\pm$1.29%	0.1237$\pm$1.35%	0.1252$\pm$1.32%	0.1266$\pm$0.88%	0.1204$\pm$1.30%	0.1300$\pm$1.32%	0.1275$\pm$1.32%
屋顶	0.0738$\pm$0.77%	0.0530$\pm$0.94%	0.0664$\pm$0.99%	0.0631$\pm$0.92%	0.0622$\pm$0.99%	0.0668$\pm$0.99%	0.0433$\pm$0.95%
金属	0.1730$\pm$1.19%	0.1187$\pm$1.27%	0.1322$\pm$1.25%	0.1268$\pm$1.24%	0.1372$\pm$1.25%	0.1298$\pm$1.25%	0.1162$\pm$1.29%
土壤	0.0193$\pm$0.27%	0.0135$\pm$0.19%	0.0143$\pm$0.20%	0.0136$\pm$0.19%	0.0149$\pm$0.24%	0.0137$\pm$0.21%	0.0115$\pm$0.20%
平均	0.1152$\pm$0.26%	0.1022$\pm$0.33%	0.1100$\pm$0.32%	0.1094$\pm$0.39%	0.1080$\pm$0.34%	0.1134$\pm$0.32%	0.1015$\pm$0.34%

下载: 导出CSV 

| 显示表格

表  7  各算法在Urban数据集上的RMSE和运行时间对比

Tab.  7.  Comparison of the RMSE values and runtimes of various algorithms on the Urban dataset

	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
RMSE	0.1269$\pm$0.40%	0.1188$\pm$0.34%	0.1235$\pm$0.41%	0.1231$\pm$0.35%	0.1225$\pm$0.39%	0.1240$\pm$0.34%	0.1150$\pm$0.35%
时间/s	43.3495	243.4455	25.3557	522.4458	361.6601	247.2024	170.4813

下载: 导出CSV 

| 显示表格

图  11  ASSC-WRNMF在Urban数据集上提取的端元与真实端元的对比

Fig.  11.  Comparison between endmembers extracted using the ASSC-WRNMF algorithm and real endmembers on the Urban dataset

下载: 全尺寸图片 幻灯片

图  12  ASSC-WRNMF在Urban数据集上估计丰度与真实丰度的对比

Fig.  12.  Comparison between the abundance estimated by the ASSC-WRNMF algorithm and the real abundance on the Urban dataset

下载: 全尺寸图片 幻灯片

（3）此外，为进一步验证本算法对图像边缘部分的处理效果和性能，对两个真实数据的部分区域单独进行对比。对比范围包含边缘较多区域和无边缘区域，其中JasperRidge数据集的三个区域如图13所示，区域尺度从区域一到区域三分别为30、25和50；Urban数据集的四个区域如图14所示，区域尺度从区域一到区域四分别为100、50、75和100。两个真实数据集部分区域的RMSE对比结果如表8和表9所示，最优结果用粗体表示。从表中可以看出，本文算法在处理图像边缘部分时有较大优势，并且在无边缘区域性能同样领先，并且对比其他结合空间信息的算法如SSWNMF、L₂₁NMF-SSR、WRNMF和SGNMF性能更好。综合以上实验，充分说明了本文算法在处理复杂高光谱图像时具有优越性。

图  13  JasperRidge数据集上三个不同的区域

Fig.  13.  Three different regions on the JasperRidge dataset

下载: 全尺寸图片 幻灯片

图  14  Urban数据集上四个不同的区域

Fig.  14.  Four different regions on the Urban dataset

下载: 全尺寸图片 幻灯片

表  8  各算法在JasperRidge数据集上不同区域的性能对比

Tab.  8.  Performance comparison of various algorithms in different regions on the JasperRidge dataset

区域	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
区域一	0.1982$\pm$0.45%	0.1840$\pm$0.28%	0.1887$\pm$0.43%	0.1630$\pm$0.47%	0.1809$\pm$0.23%	0.1681$\pm$0.33%	0.1409$\pm$0.38%
区域二	0.0575$\pm$0.50%	0.0601$\pm$0.33%	0.0571$\pm$0.38%	0.0587$\pm$0.34%	0.0564$\pm$0.42%	0.0570$\pm$0.51%	0.0560$\pm$0.29%
区域三	0.1238$\pm$0.43%	0.1094$\pm$0.30%	0.1152$\pm$0.31%	0.0964$\pm$0.32%	0.1082$\pm$0.48%	0.0992$\pm$0.37%	0.0905$\pm$0.43%

下载: 导出CSV 

| 显示表格

表  9  各算法在Urban数据集上不同区域的性能对比

Tab.  9.  Performance comparison of various algorithms in different regions on the Urban dataset

区域	L1/2-NMF	SGNMF	RONMF	WRNMF	L21NMF-SSR	SSWNMF	ASSC-WRNMF
区域一	0.2155$\pm$0.35%	0.2157$\pm$0.38%	0.2164$\pm$0.26%	0.2136$\pm$0.35%	0.2155$\pm$0.32%	0.2148$\pm$0.25%	0.2070$\pm$0.38%
区域二	0.1270$\pm$0.40%	0.1270$\pm$0.37%	0.1271$\pm$0.52%	0.1228$\pm$0.34%	0.1268$\pm$0.53%	0.1257$\pm$0.45%	0.1152$\pm$0.36%
区域三	0.1415$\pm$0.29%	0.1414$\pm$0.27%	0.1424$\pm$0.47%	0.1396$\pm$0.40%	0.1413$\pm$0.34%	0.1406$\pm$0.31%	0.1377$\pm$0.44%
区域四	0.1936$\pm$0.41%	0.1937$\pm$0.30%	0.1950$\pm$0.35%	0.1926$\pm$0.38%	0.1937$\pm$0.27%	0.1929$\pm$0.34%	0.1894$\pm$0.30%

下载: 导出CSV 

| 显示表格

5.   结论

本文提出了一种新的基于NMF模型的ASSC-WRNMF算法，用于高光谱数据的盲源解混问题。ASSC-WRNMF算法引入加权残差因子对传统的NMF模型进行改进，提升了算法的鲁棒性，即便在较强噪声影响下，该算法仍然能够保持良好的性能。此外，提出了作用于丰度的自适应空谱约束，通过像元空谱相似度选择合适的丰度邻域，有效利用了空间及光谱信息，增强了丰度的平滑性和稀疏性。并且结合端元的物理特性，加入端元平滑约束，改善了端元光谱的平滑性。在模拟数据集、JasperRidge数据集和Urban数据集上的实验结果表明本文提出的ASSC-WRNMF算法能够获得稳定且精确的解混结果，并且对比其他6种算法能够取得更好的性能。然而，所提算法依然存在一些不足：构造自适应空谱约束需要遍历高光谱图像的像元，计算量较大。另外，ASSC-WRNMF采用的是单层NMF解混模型，未考虑深层结构信息。因此在未来的工作中可以尝试解决这些问题。